This week I've work on trying to understand how badly the velocity error, explained last week, would influence my results. A lot of the time spent this week was researching articles and books regarding the velocity model of a moving vehicle. My goal was to try to theoritically understand how a static target would be perceived as a moving one while the Atlascar was rotating, for example while making a 90 degree turn, and then compare to the bagfile information recorded. In order to better understand the theory behind this issue it is best to demonstrate it with an example of the worst case scenario. Imagine the Atlascar making a left turn at 5 km/h (1.39 m/s), the radius of said curve is 4.5 meters, stated in the Atlascar manual as the minimum radius (it is not stated from where it was measured so I assumed it was from the front inner wheel to the center of the circle), a static target is detected at 9 meters to the left from the Atlascar at t0 time (as seen on image 1). The publish frequency of the targets topic from the GNN node is approximatly 19 hz, 0.05 seconds, so we can assume that the Atlascar is travelling at approximatly 0.0731 meters per scan. Using the arc length formula (Arc length = pi * turning radius *(theta/180)) being the arc length the distance travelled by the Atlascar in a scan time interval, we get the angle rate per scan of 0.9307 degrees, wich is essencially the angular velocity per scan of the Atlascar turning. Since the data collected is referenced to the Atlascar and the target is static the same distance travelled by the target is expected, meaning that instead of moving the car we move the target, the travelled distance of the target should be the same. Using the same angle as of the Atlascar but now with the distance D in the same arc lenght formula as before we get the distance travelled by targets. We can se that due to the higher distance between the target and the center of the turn (D) the arc length is also higher. Hence the error of the velocity while turning, since if the distance travelled by the target is higher so will be its velocity wich supposedly should be the same 5 km/h because the target is static. Just think about if the target was in the center of the turn, the distance D would have been 0, and the arc length also would have been 0, therefore the relative velocity between the Atlascar and the target would again be 0 wich is not true since the Atlascar is travelling at a speed of 5 km/h.
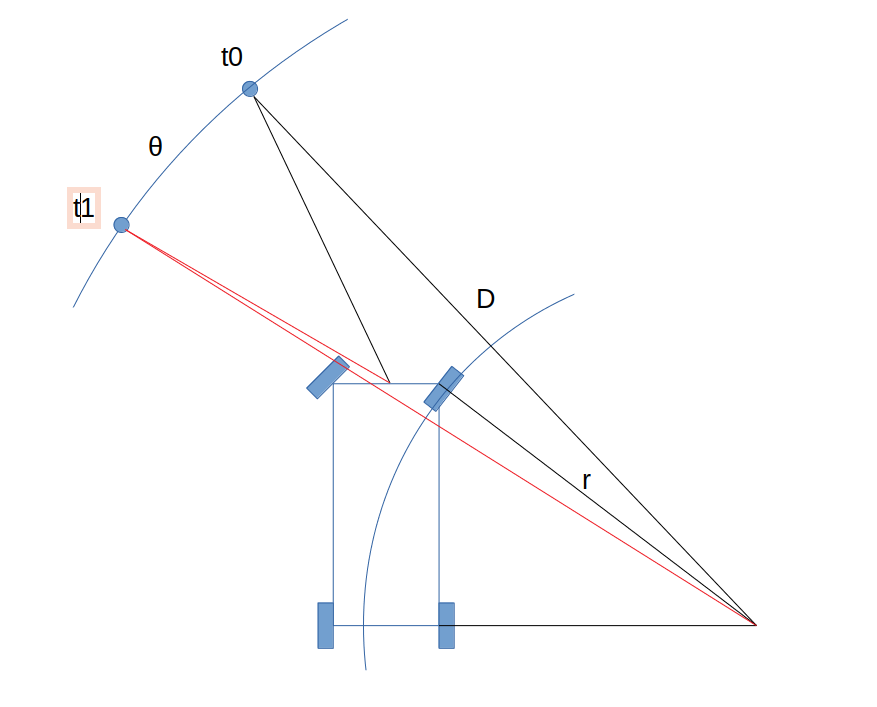
This concept is hard to grasp and many variables influence this velocity error, such as the speed of the car, the frenquency of the targets topic, although not massivly, the distance of the target to the turning center point, and the turning center point itself. This last variable is related to the car steering wheel. In order to prove this theory with the bagfile I have, I asked my colleague Diogo his bagfile wich he recorded during our ride back when I took my data. In his bagfile he recorded the velocity and the steering wheel of the Atlascar and although mine and his data weren't recorded precisely at the same time I can still get a approximation of this error efect. However this relation between the steering wheel angle, the wheel angle and turning radius is not easy to calculate. In order to prevent wheel slip and get a better control of the car while turning, all the wheel travel at different speeds, and the front wheel's make a different angle. This front wheel angle difference is called the "Ackermann steering geometry" and every car can have a different application of this geometry. In the Atlascar manual states that the car has 3.49 number of turns of the steering wheel to both sides, multiplying this by 360 we get the steering wheel angle of 1256.4 degrees, dividing by 2 we know that wheel making a full left or right the steering wheel rotates 628.2 degrees. During a turn at max steering wheel angle the inner wheel makes 45 degrees and the outer wheel 38 degrees. I know that the Atlascar uses a rack and pinion typer of steering and know that the rack moves 41.08 mm per steering wheel turn. I can use this relation and the value from the max turn of the from wheels to get a linear equation to the front wheel angles, however I didn't find any works wich confirms this, and is at the very least an approximation. The study of the velocity with Diogo's data has not yet been done, only then I can prove the theory with practice, nevertheless I can prove that there is in fact errors in the velocity since that after reviewing the velocity values after this I realised that in fact the relative velocity between the Atlascar and some know static targets were in some cases throw the roof reaches values up to 30 km/h while the Atlascar was just moving that 5 km/h mark. In some other cases with the targets with the same approximate distance to the car, the values were lower than the actual 5 km/h this is due to the location of said target being in the right side while performing a right turn (fig 2).