Although this week's main focus was to write the first chapters of the disseration, some data analysis was made for both the velocity verification and also the cpu and memory resources.
In the begining of the week I went again to Aveiro to collect more data, this time trying as best we could to start at the same time both recordings for the laser data and Diogo's velocity and steering wheel angle data. Since Diogo's package is not in the Atlas machine, and we don't have a way to download it, the best way to match the timing of the bagfiles is to start them at the same time. Being that the data is in two bagfiles, we will have issues when we playback them since there will always be a delay between the two, even with a bagfile merge, due to human reaction times. However with this temporary solution it is possible to get an approximation and after timming the bagfiles as best as I could the results were as follows.
After timming the bagfiles I started analysing the data. In Fig.1 we can see on the top left terminal the target's information (id, distance to the car, velocity) published by the GNN node. We can also see, for the same target, the calculations explained last week on the top right terminal (distance: distance from the target to the car's turning center; targetangvel: target's angular velocity; dist: car's turning center radius; carangvel: car's angular velocity). The car's current velocity and steering wheel angle is also depicted on the bottom terminal. All the distances are in meters, the velocity in km/h and the angular velocities in degrees/scan. Most of these units are not in S.I unit system, so some conversions must be made in the following calculations.
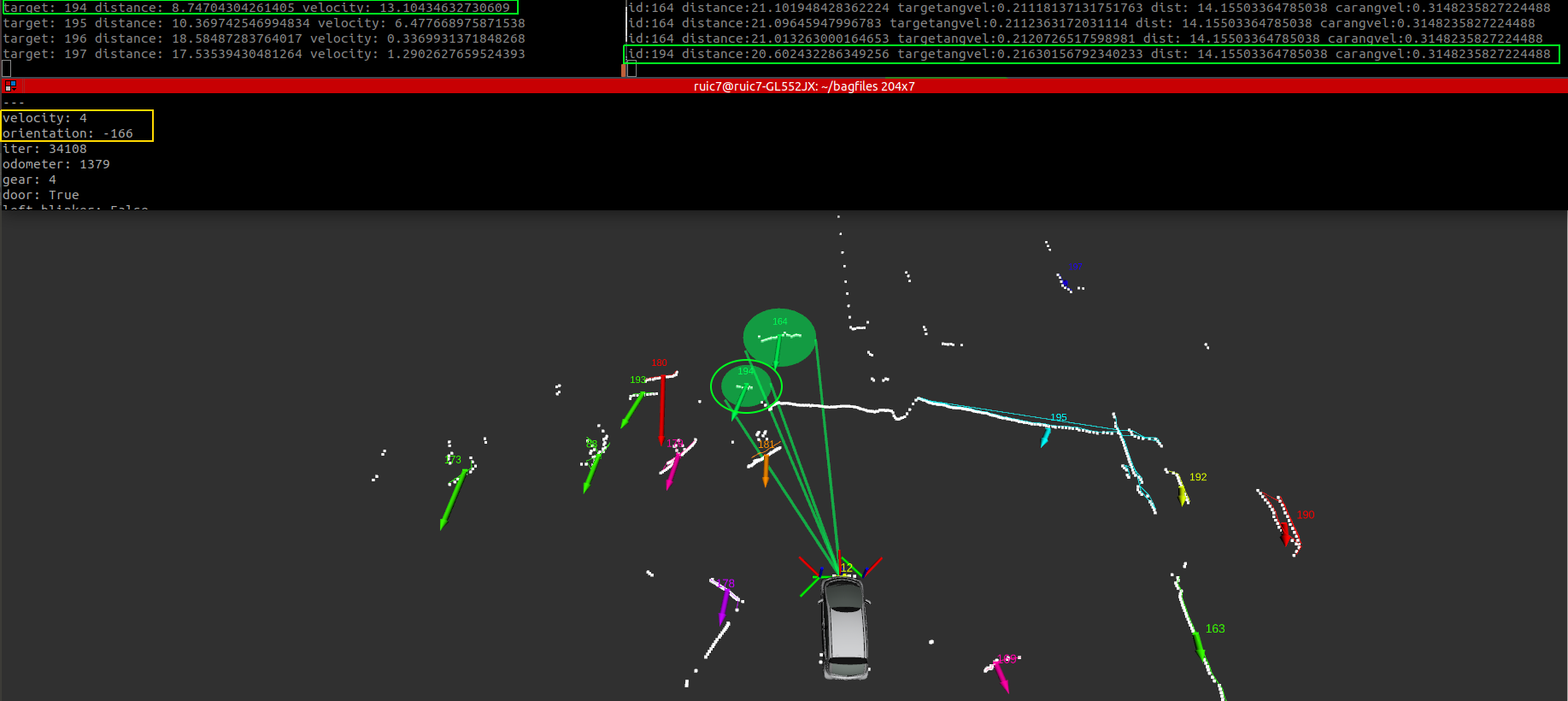

The target in question (id: 194) is a wall (Fig.2), so we know for a fact that it can't move. With that said the velocity given by the GNN should simmiliar to the actual velocity of the ATLASCAR, however as we can see it is not (GNN velocity = 13 km/h; Car velocity = 4 km/h). With distance and angular velocities calculations made and displayed on the right side terminal we can determine the approximate velocity of both the car and the target using $v= \omega * r$ being $\omega$ the angular velocity, $v$ the linear velocity and $r$ the distance. Whith this equation and remembering to convert the displayed angular velocity to rad/scan, we get the same linear velocity of approximatly 4km/h for both the car and the target. Bare in mind that these velocities are tangential velocities while rotating around the car's turning center, and for a moving target this principle does not theor apply since it's not rotating around the same point as the car. Further tests must me made to determine if in fact for a moving target the results differ.
After studying these results we can conclude that it is possible to determine if a target is in fact static by calculating it's angular velocity.
In order to get an ideia of how expensive runing all these nodes are, performance wise, a resource monitoring tool was used. The results are show on Fig.3
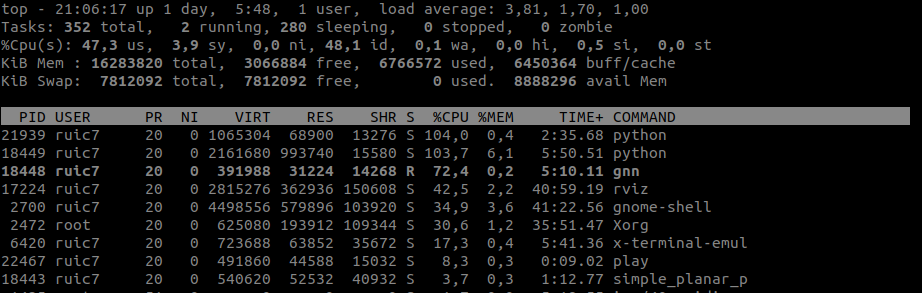
In the image we can see the two python nodes (the first one is the short term path node with 0.4% total memory used and the seconde one is VO node with 6.1% total memory used), the gnn node aswell as the simple planar pc generator. On the third row of the image is displayed the cpu usage as a percentage by the user of 47.3% wich means approximatly only 50% of the cpu capabality is used. These values seem acceptable in this stage, however I was able to detect that the VO node memory usage kept climbing (currently at 6.1%) while the number of targets increases (at the time the number of targets was about 1700). This means that if the node ran indefinitly, it will eventually run out of memory, crashing the computer. This was due to the fact that the node records every single target data and keeps it in memory. This rather basic resource monitoring was essencial to realize that the code needs to be once again reviewed to correct such issues.